Directional energy potential (SEP)

The central concept of TRR–NOTIME is the Directional Energy Potential (SEP):

$$ \vec{\varphi} = \frac{\vec{E}_{\text{directional}}}{m}, \qquad [\vec{\varphi}] = \mathrm{[m^2]} $$

Here, \( \vec{E}_{\text{directional}} \) is projectable energy in a chosen direction and \( m \) is the mass of the configuration. SEP is purely spatial and directional; no time variable is required.

Equilibrium: all outgoing directions saturated; red shows an unsaturated projection.
Equilibrium vs. Gravitational Imbalance In equilibrium, all outgoing directions are saturated: \( \sum_k \vec{\varphi}_k = \vec{0} \). A single unsaturated direction creates a net SEP projection (in red) — interpreted as gravity.
Directional compatibility between two SEP vectors and node formation threshold.
Directional Compatibility (Axiom 7) Real interaction emerges only if \( \vec{\varphi}_1 \cdot \vec{\varphi}_2 \geq \varphi_{\text{critical}}^2 \). Only mutually aligned SEP vectors form a node. The higher the compatibility \( \cos\theta \), the stronger the interaction.
Latent vacuum: nonzero SEP vectors cancel to zero net projection.
TRR Vacuum: Latent SEP Structure SEP vectors can be nonzero while cancelling each other: \( \vec{\varphi}_k \neq 0 \), yet \( \sum_k \vec{\varphi}_k = \vec{0} \). This defines a stable, silent vacuum.
Aligned SEP vectors connecting two structures (entanglement) without a net projection.
TRR Interpretation of Entanglement Entanglement arises from aligned directional SEP vectors across distance. The alignment exists without active interaction; it becomes effective when the projection is unsaturated.
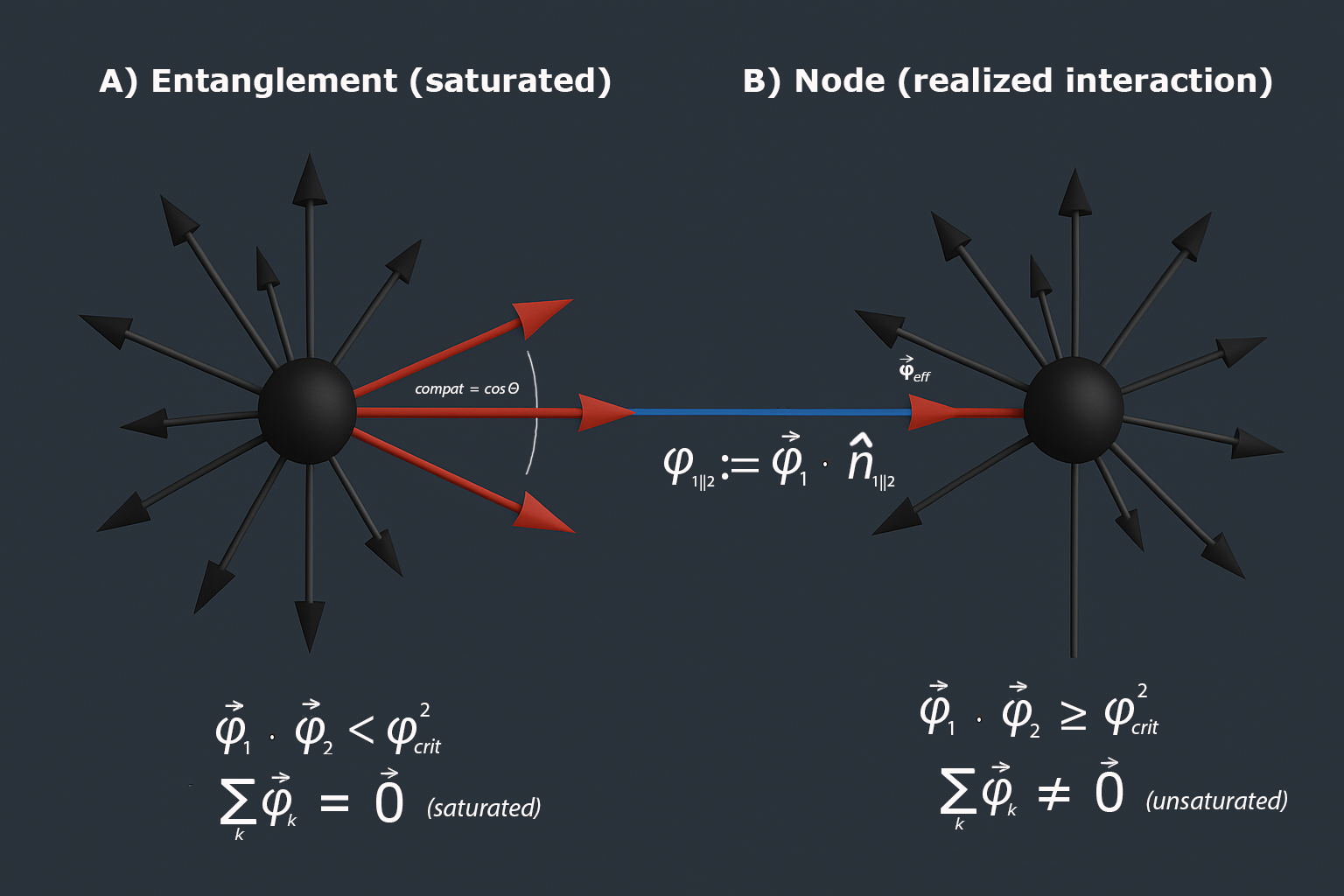
Aligned SEP vectors: saturated alignment vs. unsaturated alignment forming a realized interaction node.
Entanglement vs. Realized Node Left: directional alignment with saturation   \(\sum_k \vec{\varphi}_k=\vec{0}\), and sub-critical overlap   \(\vec{\varphi}_1\!\cdot\!\vec{\varphi}_2<\varphi_{\text{crit}}^{2}\).  — no node
Right: same alignment but unsaturated   \(\sum_k \vec{\varphi}_k\neq\vec{0}\),,  and super-critical overlap, \(\vec{\varphi}_1\!\cdot\!\vec{\varphi}_2\ge\varphi_{\text{crit}}^{2}\),  a realized interaction node with local  \(\vec{\varphi}_{\mathrm{eff}}\) along \(\hat n_{12}\).
Universality Across Scales — One Law, Two Datasets

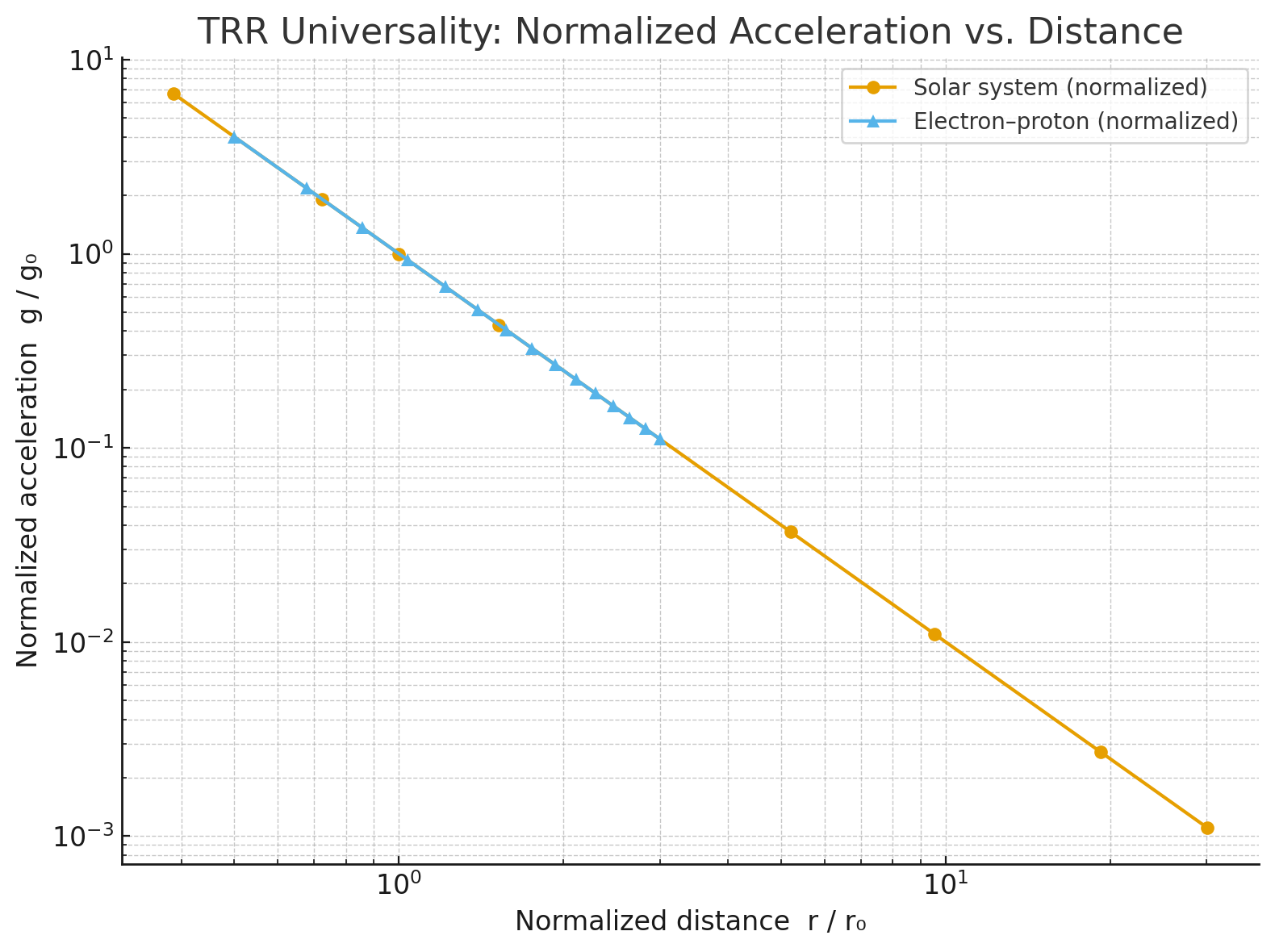
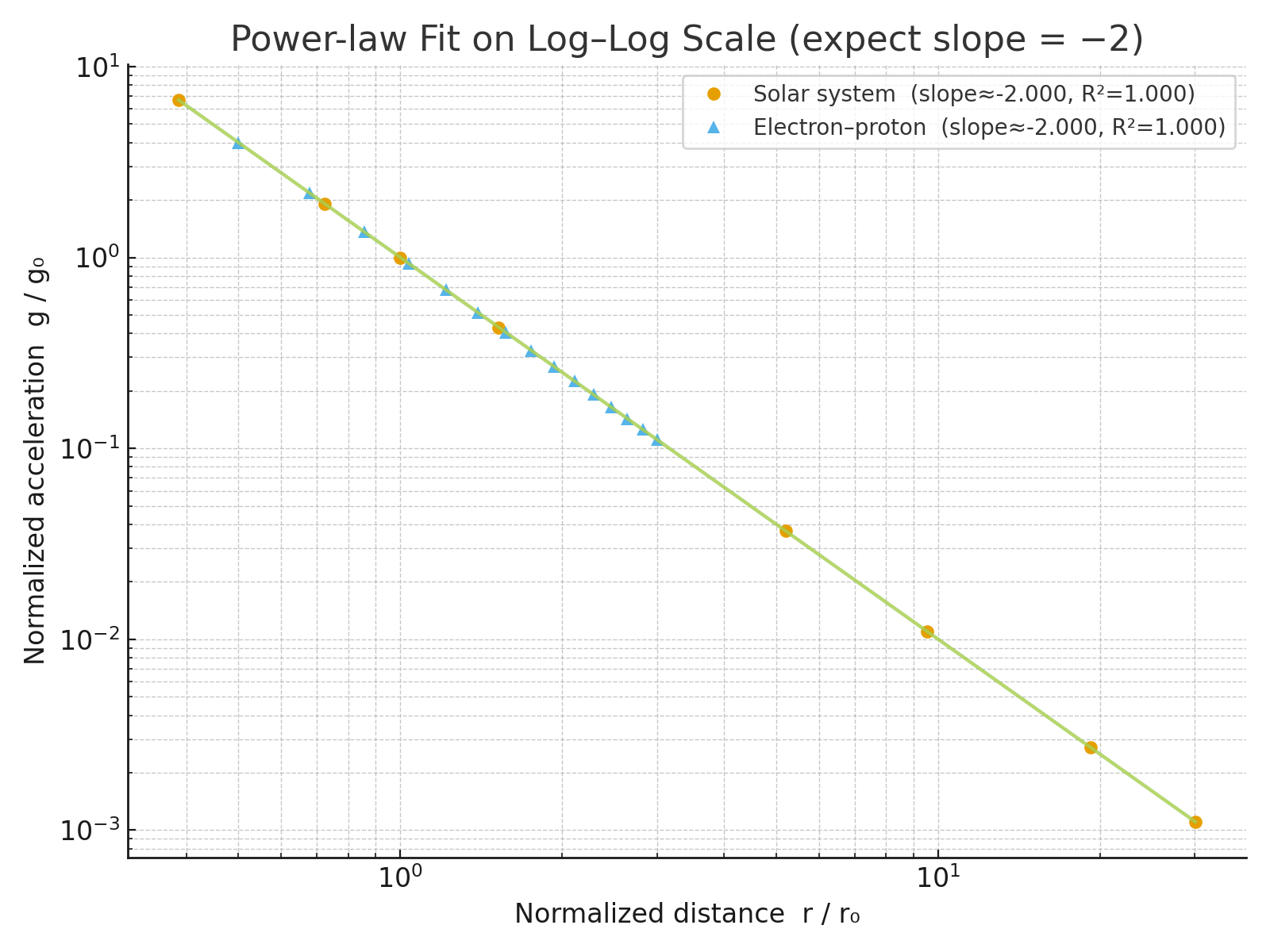
After normalizing to reference pairs \((r_0, g_0)\), the two independent datasets (solar system, electron–proton) overlap and lie on a straight line in log–log axes with slope ≈ −2, i.e. \( g_{\mathrm{norm}} = 1/r_{\mathrm{norm}}^{2} \).

  • Solar: \( r_0 = 1\,\mathrm{AU} \), \( g_0 = g(1\,\mathrm{AU}) \).
  • Micro: \( r_0 = a_0 \) (Bohr radius), \( g_0 = g(a_0) \).

Conclusion: both scale regimes obey the same \(1/r^2\) law; the difference is only the choice of \((r_0, g_0)\). This is consistent with the TRR statement \( g_{\mathrm{TRR}} = \lvert \vec{\varphi}_{\mathrm{eff}} \rvert / m \).

Normalized g/g0 vs r/r0: solar and electron–proton datasets overlap after normalization.
(A) Normalized TRR acceleration across scales
On log–log axes the combined normalized datasets form a line with slope near −2 (the 1/r^2 law).
(B) Log–log power-law consistency (slope ≈ −2)
Normalized table — applies to both datasets. References: Solar \(r_0=1\,\mathrm{AU},\ g_0=g(1\,\mathrm{AU})\); Micro \(r_0=a_0,\ g_0=g(a_0)\).
r_norm = r / r₀ g_norm = g / g₀ (= 1 / r_norm²)
0.504.0000
0.751.7778
1.001.0000
1.500.4444
2.000.2500
3.000.1111
Mapping examples (same rows, two scales):
  • Solar: Earth–Sun → \(r_{\mathrm{norm}}=1\Rightarrow g_{\mathrm{norm}}=1\). Mercury (0.387 AU) → \(r_{\mathrm{norm}}\approx0.387\Rightarrow g_{\mathrm{norm}}\approx 6.67\). Neptune (30.06 AU) → \(r_{\mathrm{norm}}\approx30.06\Rightarrow g_{\mathrm{norm}}\approx 0.0011\).
  • Micro: \(r=a_0\) (Bohr) → \(r_{\mathrm{norm}}=1\Rightarrow g_{\mathrm{norm}}=1\). \(r=0.5\,a_0\) → \(g_{\mathrm{norm}}=4\). \(r=2\,a_0\) → \(g_{\mathrm{norm}}=0.25\).
Interpretation: both scales follow \(g_{\mathrm{norm}}=1/r_{\mathrm{norm}}^{2}\); only the references \(r_0, g_0\) differ.

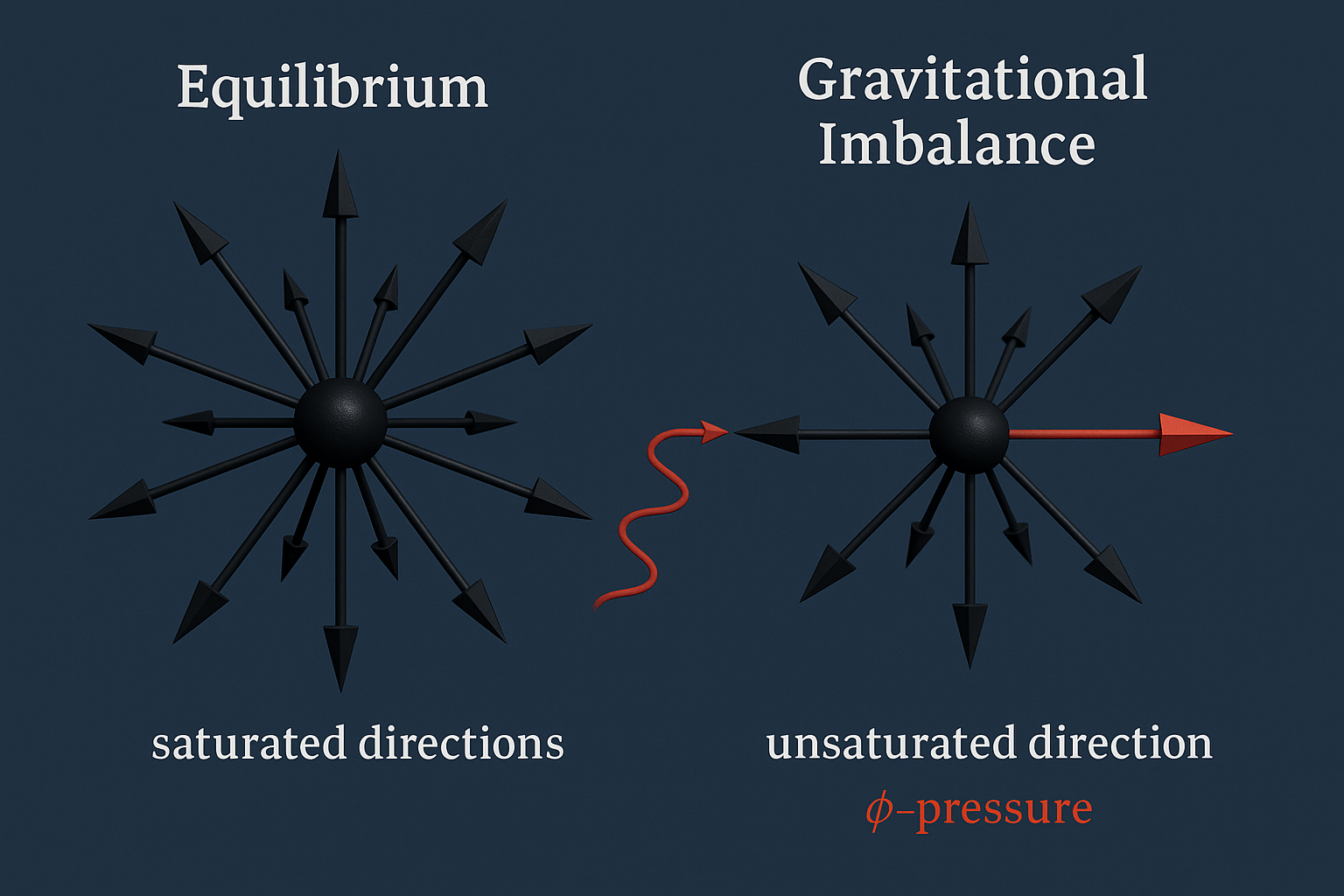
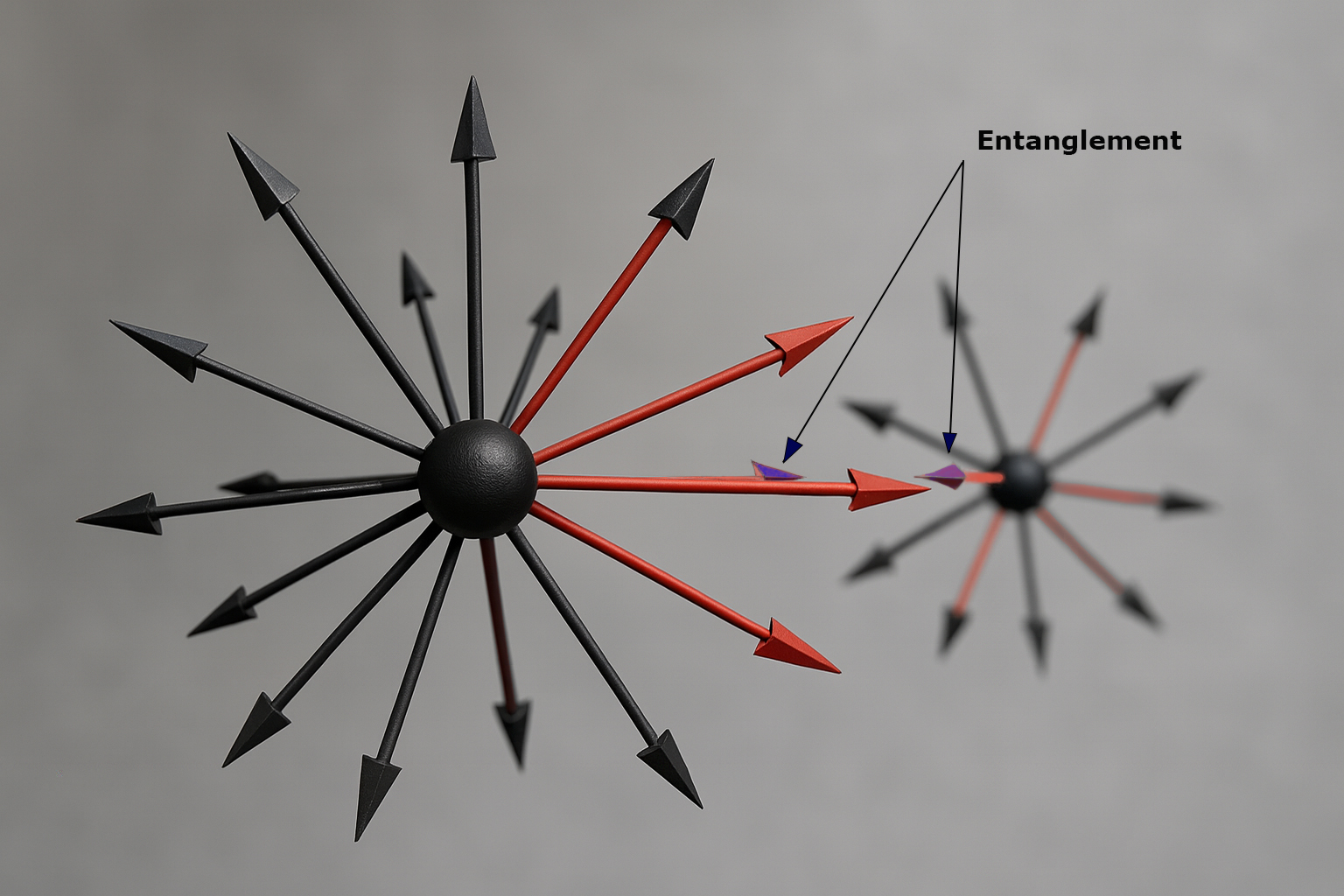
Both gravity and entanglement are the same directional SEP structure; entanglement is aligned-but-saturated (no net projection), while gravity is the unsaturated net projection of the same alignment.

TRR–NOTIME Casimir: lower directional compatibility inside the gap (low interference) → net inward pressure; outside the plates, projectional over-saturation of directions.
Casimir in TRR–NOTIME (Directional SEP Saturation) Inside the plates: fewer admissible directions → reduced SEP compatibility. Outside: projectional over-saturation of directions. Result: a net inward pressure, reproducing the inverse-quartic scaling without time, forces, or vacuum fluctuations. DOI 10.5281/zenodo.17265344
$$ P_{\mathrm{Casimir}}^{\mathrm{TRR}}(d) = C_{\mathrm{proj}}\,\frac{1}{d^{4}} $$
$$ \log_{10}\!\lvert P\rvert = \mathrm{const} - 4\,\log_{10}\! d $$

\(C_{\mathrm{proj}}\) is a combinatorial projection constant fixed by the chosen SEP-density unit; it reproduces QED-level magnitudes without time, forces, or vacuum fluctuations (see the DOI above).

Methodological note

All predictions on this page are computed purely in the SEP space. Where compared to observation (ISS, GPS, redshift), results are translated without time.